数组
列举数组的算法题。
1. 两数求和
真题描述:给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那两个整数,并返回他们的数组下标。
示例:给定 nums = [2, 7, 11, 15], target = 9。
结果:因为 nums[0] + nums[1] = 2 + 7 = 9,所以返回 [0, 1]。
对于这个题目,大家首先会想到一个“简单粗暴”的方法,就是两层循环,然后将每层的值相加判断。但是这样的时间复杂度是 O(n^2)。
事实上,我们完全没有必要用两层循环,这样会让算法的时间成倍增加。我们可以用“空间换取时间”的思想,用一层循环解决这个问题,如下:
const gethe = (nums, target) => {let diffs = {};for (let i = 0; i < nums.length; i++) {if (diffs[target - nums[i]]) {return [i, diffs[target - nums[i]]];}diffs[nums[i]] = i;}return null;};
代码中申请一个 diffs 对象来存储循环过的值和下标,然后用求差的方式判断该对象中是否有符合条件的属性,如果有则返回各自的下标。
小提示:几乎所有的求和问题,都可以转化为求差问题解决。
2. 合并有序数组
真题描述:给定两个有序整数数组 nums1 和 nums2,请将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。
输入:
nums1 = [1,2,3]
nums2 = [2,5,6]
输出:[1,2,2,3,5,6]
注意,要将数组 nums2 合并到 nums1 中,不是返回新数组,因此可以通过 splice 函数实现:
nums1.splice(nums1.length, 0, ...nums2);nums1.sort();
如果不使用快捷方法,只用遍历实现的话,应该怎么做呢?就要用到双指针法。
双指针法,就是定义两个变量,分别指向两个数组的最后一位索引。接着在循环中执行比较,当其中一个数组满足比较条件时,指针向前移动一位,直到某一个数组移动到第一位。
const merge = function (nums1, nums2) {// 初始化两个指针的指向,初始化 nums1 尾部索引klet i = m - 1,j = n - 1,k = m + n - 1;// 当两个数组都没遍历完时,指针同步移动while (i >= 0 && j >= 0) {// 取较大的值,从末尾往前填补if (nums1[i] >= nums2[j]) {nums1[k] = nums1[i];i--;k--;} else {nums1[k] = nums2[j];j--;k--;}}// nums2 留下的情况,说明都是小值,放到最前面即可while (j >= 0) {nums1[k] = nums2[j];k--;j--;}};
代码中的比较逻辑是,判断指针处哪个数组对应的值大,然后该指针向前移动,并将大的值添加到最后面,这样从后到前遍历一次,就会合并成一个有序的数组。
3. 三数求和
真题描述:给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:给定数组 nums = [-1, 0, 1, 2, -1, -4]
结果:[ [-1, 0, 1], [-1, -1, 2] ]
如果直接遍历的话,实现上面的需求要做三层循环。我们依然用空间换时间的思想,尽可能的减少遍历。
具体方法,仍然是使用指针来缩小搜索的范围。对于三数求和,我们使用 “固定一个,移动两个”的方式,如图:
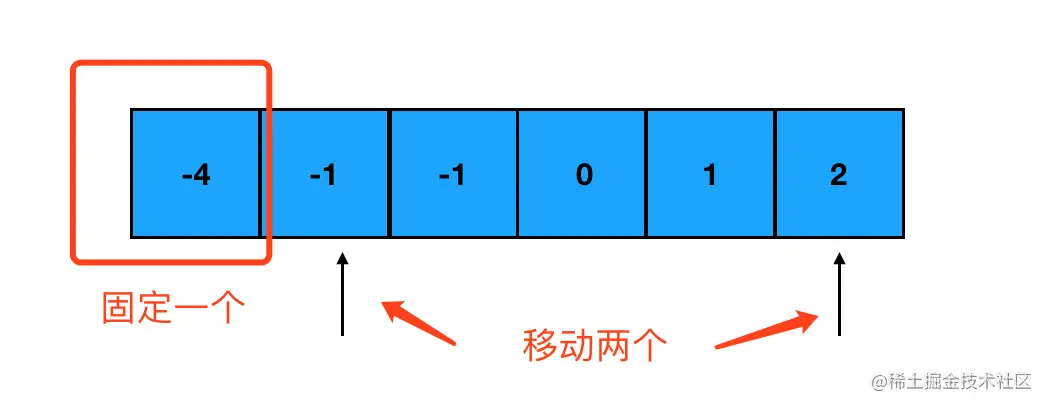
每次移动指针,就计算一次固定值加上两个指针指向数字之和,是否等于 0。如果是,那我们就得到了一个目标组合;如果不是,则继续移动指针。
const threeSum = (nums) => {num.sort();let res = [];let leng = nums.length;for (let i = 0; i < leng - 2; i++) {let j = i + 1;let k = leng - 1;while (j < k) {let diff = nums[i] + nums[j] + nums[k];if (diff == 0) {res.push([nums[i], nums[j], nums[k]]);} else if (diff > 0) {k--;} else {j++;}}}};
代码中,将两个指针分别指向数组的前后位置,依次向中间移动,这种方式叫做“对撞指针”,可以避免多余的遍历。
4. 二分查找
给定一个 元素升序的、无重复数字 的整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标(下标从 0 开始),否则返回 -1。
function search(nums, target) {let left = 0;let right = nums.length - 1;while (left <= right) {let mid = Math.floor((left + right) / 2);if (nums[mid] === target) {return mid; // 目标值找到了,返回它的索引} else if (nums[mid] < target) {left = mid + 1; // 在右半边查找} else {right = mid - 1; // 在左半边查找}}return -1; // 没有找到目标值}
下面是我自己写的递归方案:
// write code herefunction search(nums, target) {const subfun = (arrs) => {if (arrs.length == 1) {return nums.indexOf(arrs[0]);}let cent = Math.floor(arrs.length / 2);if (arrs[cent] == target) {return nums.indexOf(target);}if (arrs[cent] > target) {arrs = arrs.slice(0, cent);} else {arrs = arrs.slice(cent);}return subfun(arrs);};return subfun(nums);}
5. 写一个并发的任务队列
- 构造函数接收一个表示最大并发数的参数
- 有一个 addTask 方法,用于添加任务(函数)到队列
- 有一个 run 方法,开始执行任务队列
- 任务执行时遵循先进先出(FIFO)原则
- 当有任务执行完毕时,如果还有未执行的任务,应立即开始执行新的任务
- 所有任务执行完毕后,调用传入的回调函数
class TaskQueue {constructor(concurrency: number) {this.concurrency = concurrency; // 最大并发数// 实现构造函数}concurrency = 1;queues: any[] = []; // 任务队列addTask(task: any) {// 实现添加任务的方法this.queues.push(task);}run(callback: () => void) {if (this.queues.length == 0) {return callback();}// 实现运行任务队列的方法let multi_queues = [];for (let i = 0; i < this.concurrency; i++) {let q = this.queues.pop();if (q) {multi_queues.push(q);}}Promise.all(multi_queues).then(() => {this.run(callback);}).catch(() => {// 没调用 reject 这行可能不会触发this.queues.concat(multi_queues); // 失败后重新加入队列,下次执行});}}